About hydrogen
Hydrogen Isotopes
Hydrogen [1] (hydrogenium, udwr = the water, gennein = genesis, to give birth) is the first element in the periodic table of the elements having the atomic number 1 and the electron configuration 1s1. Hydrogen was prepared many years before it was recognised as a distinct substance by Cavendish in 1766 and it was named by Lavoisier. Hydrogen is the most abundant of all elements in the universe, and it is thought that the heavier elements were, and still are, being built from hydrogen and helium. It has been estimated that hydrogen makes up more than 90% of all the atoms or 75% of the mass of the universe. It is found in the sun and most stars, and plays an important part in the proton-proton reaction and carbon-nitrogen cycle, which accounts for the energy of the sun and stars. It is thought that hydrogen is a major component of the planet Jupiter and that at some depth in the planet’s interior the pressure is so great that solid molecular hydrogen is converted into solid metallic hydrogen.
The ordinary isotope of hydrogen, H is known as Protium [2] and has an atomic weight of 1.0078 (1 proton and 1 electron). In 1932, Urey [3] announced the preparation of a stable isotope, Deuterium (D) with an atomic weight of 2.0140 (1 proton and 1 neutron, 1 electron). Two years later [4] an unstable isotope, Tritium (T), with an atomic weight of 3.0161 (1 proton and 2 neutron, 1 electron) was discovered . Tritium has a half-life time of 12.5 years [5]. Deuterium is found in 0.017% of all hydrogen isotopes. Tritium atoms are also present 10-18% of all hydrogen isotopes as a result of natural processes in the atmosphere, as well as from fallout from past atmospheric nuclear weapons tests and the operation of nuclear reactors and fuel reprocessing plants.
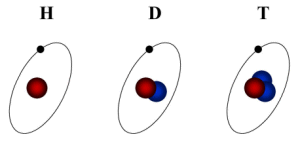
Fig. Schematic representation of hydrogen or protium (H), deuterium (D) and tritium (T)
|
CAS No. |
1H
[12 385-13-6] |
2D
[16873-17-9] |
3T
[15086-10-9] |
| atomic mass [u] | 1.007825 | 2.0140 | 3.01605 |
| natural abundance [%] | 99.985 | 0.015 | » 10-18 |
| half life time [a] | 12.26
b 0.01861 MeV |
||
| ionisation energy [eV] | 13.5989 | 13.6025 | 13.6038 |
| thermal neutron capture cross section [10-24 cm2] | 0.322 | 0.51·10-3 | <6·10-6 |
| nuclear spin [h/2p] | +½ | +1 | +½ |
| nuclear magnetic moment, nuclear magnetons [µN] | +2.79285 | +0.85744 | 2.97896 |
Tab. Atomic data of hydrogen isotopes.
The atomic radius of the free hydrogen atom in the ground state , the Bohr radius is a0 = h2/(p2·e2·m) = 0.529Å and the covalent atomic radius of hydrogen in crystal structures is between 30 and 35 pm.
The Hydrogen Molecule
The isotopes H, D and T form diatomic molecules. The interaction potential energy of two hydrogen atoms goes through a minimum at a certain interatomic distance when two electrons form a singlet state 1Sg+, namely, the state with a total electron spin equal to zero (the combination of two electrons with opposite spin). The energy of the tripplet state 3Su+,having a total electron spin of unity, increases when two hydrogen atoms with parallel spin approach each other. Hydrogen atoms of opposite spin exist in equal numbers, and readily combine in pairs to form singlet state molecules. The formation of molecules can be suppressed by applying a strong magnetic field to an atomic hydrogen gas.
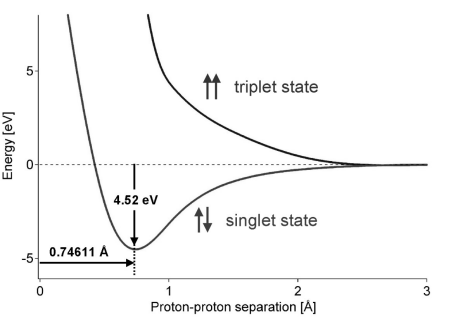
Fig. The singlet state exhibits a minimum in the interaction potential energy for a proton-proton separation of 0.74611 Å. The binding energy is 4.52 eV, i.e. 2.26 eV per H atom (218.1 kJ·mol-1H) to separate the H-H bond.
Quantum mechanics requires that the wave function of a molecule must be antisymmetric with respect to the interchange of the space coordinates of two fermions (spin = ½), and symmetric for the interchange of bosons (spin = 1). Thus the wave function of a H2 (T2) molecule should be antisymmetric on interchange of two protons (tritons), and that D2 symmetric on interchange of two deuterons. There are a total of (2I+1)2 combinations of nuclear spin states for two identical nuclei of spin I, of which (2I+1)(I+1) states are symmetric and (2I+1)I are antisymmetric with respect to the interchange of the nuclei. Consequently there are two kinds of hydrogen molecules in the singlet state, namely, ortho-hydrogen (symmetric, with parallel nuclear spins ) and para-hydrogen (antisymmetric, with antiparallel nuclear spins ¯).
When the nuclei are fermions, as in the case of protons (tritons), the symmetric nuclear spin states must be coupled with the antisymmetric rotational states (odd J) and the antisymmetric nuclear spin states must be coupled with the symmetric rotational states (even J).
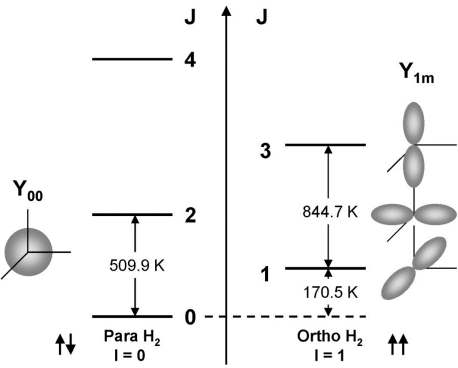
Fig. Energies and wave functions of rotational states (J) of a para-hydrogen and an ortho-hydrogen molecule. The total nuclear spin I is 0 or 1, respectively and the rotational quantum number is 0, 1, 2… [7]
The population ratio of ortho-hydrogen to para-hydrogen in thermal equilibrium is given by
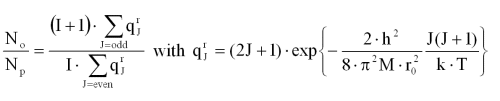
The following forms of hydrogen are distinguished: o-H2 ortho-hydrogen, p-H2 para-hydrogen, e-H2 equilibrium hydrogen and n-H2 normal hydrogen. e-H2, e-D2, and e-T2 all correspond to the equilibrium concentration of definite temperatures. n-H2 is a mixture of the equilibrium concentration of ortho- and para-hydrogen at a temperature of 293.15 K (20°C), i.e. 25 mol% p-H2 and 75 mol% o-H2. At low temperature p-H2, o-D2 and p-T2 can be present in a virtually pure state. The conversion of o-H2 to p-H2 is exothermic and a function of temperature. When hydrogen is cooled from room temperature (RT) to the normal boiling point (nbp = 21.2K) the ortho hydrogen converts from an equilibrium concentration of 75% at RT to 50% at 77K and 0.2% at nbp.
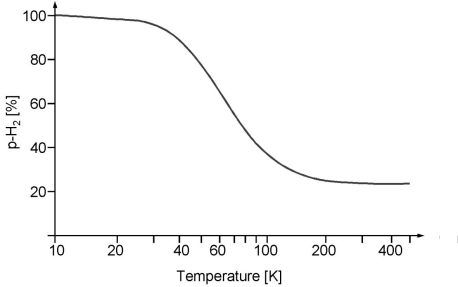
Fig. Amount of para-hydrogen (p-H2) in the equilibrium composition e-H2 as a function of temperature.
The self conversion rate is an activated process and very slow, the half-life time of the conversion is greater than one year at 77K. The conversion reaction from ortho- to para-hydrogen is exothermic and the heat of conversion is also temperature dependent [9]. At 300K the heat of conversion is 270 kJ·kg-1 and increases as the temperature decreases, where it reaches 519 kJ·kg-1 at 77K. At temperatures lower than 77K the enthalpy of conversion is 523 kJ·kg-1 and almost constant. The enthalpy of conversion is greater than the latent heat of vaporisation (DHV = 451.9 kJ·kg-1) of normal and para hydrogen at the nbp. If the unconverted normal hydrogen is placed in a storage vessel, the enthalpy of conversion will be released in the vessel, which leads to the evaporation of the liquid hydrogen. The transformation from ortho- to para-hydrogen can be catalysed by a number of surface active and paramagnetic species, e.g. n-H2 can be adsorbed on charcoal cooled with liquid hydrogen and desorbed in the equilibrium mixture (e-H2). The conversion [8] may take only a few minutes if a highly active form of charcoal is used. Other suitable ortho-para catalysts are metals such as tungsten, nickel, or any paramagnetic oxides [10] like chromium or gadolinium oxides. The nuclear spin is reversed without breaking the H-H bond.
| n-H2 | n-D2 | n-T2 | HD | HT | DT | |
| CAS No. | 1333-74-0 | 7782-39-0 | 10028-17-8 | 13983-20-5 | 14885-60-0 | 14885-61-1 |
| molecular mass [u] | 2.016 | 4.029 | 6.034 | 3.022 | 4.025 | 5.022 |
| bond length [pm] | 74.6 | 74.2 | 74.1 | |||
| dissociation energy [eV] | 4.473 | 4.552 | 4.510 | |||
| triple point | ||||||
| temperature [K] | 13.96 | 18.73 | 20.62 | 16.60 | 17.63 | 19.71 |
| pressure [kPa] | 7.3 | 17.1 | 21.6 | 12.8 | 17.7 | 19.4 |
| criticle point | ||||||
| temperature [K] | 32.98 | 38.35 | 40.44 | 35.91 | 37.13 | 39.42 |
| pressure [kPa] | 1.31 | 1.67 | 1.85 | 1.48 | 1.57 | 1.77 |
| normal boiling point [K] | 20.39 | 23.67 | 25.04 | 22.13 | 22.92 | 24.38 |
| density at n-b.p. | ||||||
| rL [kg·m-3] | 70.811 | 162.50 | 260.17 | 114.80 | 158.62 | 211.54 |
| rV [kg·m-3] | 1.316 | 2.230 | 3.136 | 1.802 | 2.310 | 2.694 |
| Heat of vaporization [J·mol-1] at 25K | 825 | 1175 | 1400 | 1000 | 1100 | 1290 |
Fig. Physical properties of molecules of the hydrogen isotopes.
Physical Properties
In hydrogen, the interaction between molecules is weak as compared to other gases, therefore the critical temperature is low (Tc = 33.0 K). The melting curve, the solid-liquid boundary in a p-T diagram, has been determined by several groups [11] for p-H2 and n-D2. The following functions were determined by least-squeres fitting:
pm = -51.49 + 0.1702·(Tm + 9.689)1.8077 for H2
pm = -51.87 + 0.3436·(Tm)1.691 for D2
where pm is in MPa and Tm in Kelvin. The melting pressure for D2 is by about 4% lower than for H2 at a given temperature.
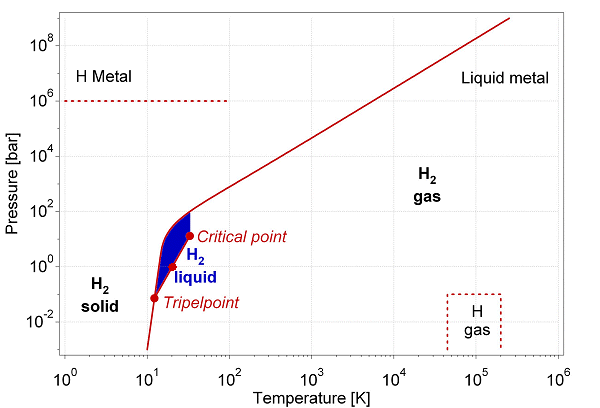
Fig. Primitive phase diagram for hydrogen [12]
| Temperature [K] | Vapor pressure [kPa] | Density | [kg/m3] | |
| rS | rL | rG | ||
| 1 | 11·10-37 | 89.024 | ||
| 5 | 4.76·10-3 | 88.965 | ||
| 10 | 255.6 | 88.136 | 0.006 | |
| 12 | 1837 | 87.532 | 0.037 | |
| 13.803a | 7.0 | 86.503 | 77.019 | 0.126 |
| 20 | 93.5 | 71.086 | 1.247 | |
| 20.268b | 101.3 | 70.779 | 1.338 | |
| 30 | 822.5 | 53.930 | 10.887 | |
| 32.976c | 1293 | 31.43 |
Fig. Vapor pressure and density of p-hydrogen at low temperatures, a Triple point, b101.3 kPa, cCritical point.
At zero pressure, hydrogen (H2, D2) solidify in the hexagonal closest-packed (hcp) structure. Data for p-H2 [14] are: a = 375 pm, c/a = 1.633, molar volume 22.56 cm3·mol-1. The spherical J = 0 species (p-H2, o-D2) undergo a structural transition below 4 K where the rotational motion of the molecules is quenched, and the molecules are located on the fcc lattice (space group Pa3) with their axes oriented along the body diagonals.
At very high pressures (>2·1011 Pa), solid hydrogen is expected [15] to transform from a diatomic molecular phase to a monatomic metallic phase with a density > 1000 kg·m-3. This phase may become a high-temperature superconductor [16].
Fig. Vapor pressure and density of p-hydrogen at low temperatures, a Triple point, b101.3 kPa, cCritical point.
At zero pressure, hydrogen (H2, D2) solidify in the hexagonal closest-packed (hcp) structure. Data for p-H2 [14] are: a = 375 pm, c/a = 1.633, molar volume 22.56 cm3·mol-1. The spherical J = 0 species (p-H2, o-D2) undergo a structural transition below 4 K where the rotational motion of the molecules is quenched, and the molecules are located on the fcc lattice (space group Pa3) with their axes oriented along the body diagonals.
At very high pressures (>2·1011 Pa), solid hydrogen is expected [15] to transform from a diatomic molecular phase to a monatomic metallic phase with a density > 1000 kg·m-3. This phase may become a high-temperature superconductor [16].
| p-H2 | n-H2 | |
| Triple point (T = 13.803 K, p = 7.04 kPa) | ||
| Temperature [K] | 13.803 | 13.957 |
| Pressure [kPa] | 7.04 | 7.2 |
| Density (solid) [kg·m-3] | 86.48 | 86.71 |
| Density (liquid) [kg·m-3] | 77.03 | 77.21 |
| Density (vapor) [kg·m-3] | 0.126 | 0.130 |
| Heat of melting DHm [J·mol-1] | 117.5 | |
| Heat of sublimation DHV [J·mol-1] | 1022.9 | |
| Enthalpy DH0 [J·mol-1] | -740.2 | |
| Entropy DS0 [J·mol-1·K-1] | 1.49 | |
| Thermal conductivity [W m-1K-1] | 0.9 | |
| Dielectric constant | 1.286 | |
| Boiling point at p = 101.3kPa | ||
| Temperature Tb [K] | 20.268 | 20.39 |
| Heat of vaporization DHV [J·mol-1] | 898.30 | 899.1 |
Tab. 2.1.4. Physical properties of para-hydrogen (p-H2) and normal-hydrogen (n-H2) at the triple- and normal boiling point.
| p-H2 | n-H2 | |
| Liquid phase at boiling point | ||
| Density [kg·m-3] | 70.78 | 70.96 |
| Specific heat capacity cp [J·mol-1·K-1] | 19.70 | 19.7 |
| Specific heat capacity cV [J·mol-1·K-1] | 11.60 | 11.6 |
| Enthalpy DH0 [J·mol-1] | -516.6 | -548.3 |
| Entropy DS0 [J·mol-1·K-1] | 16.08 | 34.92 |
| Viscosity [mPa·s] | 13.2·10-3 | 13.3·10-3 |
| Velocity of sound [m s-1] | 1089 | 1101 |
| Thermal conductivity [W m-1K-1] | 98.92·10-3 | 100·10-3 |
| Compressibility factor | 0.01712 | 0.01698 |
| Vapor phase at boiling point | ||
| Density [kg·m-3] | 1.338 | 1.331 |
| Specific heat capacity cp [J·mol-1·K-1] | 24.49 | 24.60 |
| Specific heat capacity cV [J·mol-1·K-1] | 13.10 | 13.2 |
| Enthalpy DH0 [J·mol-1] | 381.61 | 1447.4 |
| Entropy DS0 [J·mol-1·K-1] | 60.41 | 78.94 |
| Viscosity [mPa·s] | 1.13·10-3 | 1.11·10-3 |
| Velocity of sound [m s-1] | 355 | 357 |
| Thermal conductivity [W m-1K-1] | 16.94·10-3 | 16.5·10-3 |
| Compressibility factor | 0.906 | 0.906 |
| Critical point | ||
| Temperature [K] | 32.976 | 33.19 |
| Pressure [MPa] | 1.29 | 1.325 |
| Density [kg·m-3] | 31.43 | 30.12 |
| Properties at STP (T = 273.15 K, p = 101.3 kPa) | ||
| Density [kg·m-3] | 0.0899 | 0.0899 |
| Specific heat capacity cp [J·mol-1·K-1] | 30.35 | 28.59 |
| Specific heat capacity cV [J·mol-1·K-1] | 21.87 | 20.3 |
| Viscosity [mPa·s] | 8.34·10-3 | 8.34·10-3 |
| Velocity of sound [m s-1] | 1246 | 1246 |
| Thermal conductivity [W m-1K-1] | 182.6·10-3 | 173.9·l0-3 |
| Dielectric constant | 1.00027 | 1.000271 |
| Compressibility factor | 1.0005 | 1.00042 |
| Prandtl number | 0.6873 | 0.680 |
Fig. Physical properties of liquid and gaseous para-hydrogen (p-H2) and normal-hydrogen (n-H2).
The equation of state
Among the most fundamental knowledge about the thermodynamic properties of hydrogen is the equation of state (EoS), namely, the volume as a function of pressure and temperature V(p,T). Once the EoS is known, all the thermodynamic quantities can be calculated. The Gibbs free energy G(p,T) and entropy S(p,T) can be obtained by integration

The enthalpy is then given by
![]()
At low ga density, al real gases tend to obey their ideal gas law
where p is the absolute pressure, V the volume, n the number of gas molecules and R the gas constant (8.314 J·mol-1·K-1). In a real gas, however, the gas molecules occupy a certain volume the „excluded volume“ b and the molecules interact by means of the Van der Waals force (dipole interaction), which is expressed with the „interaction strength“ a. The Van der Waals equation for real gases is therefore
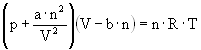
with the appropriate parameter for hydrogen: a(H2) = 2.476·10-2 m6·Pa·mol-2 and b(H2) = 2.661·10-5 m3·mol-1. The pressure as a function of the volume of a real gas is given by
![]()
The p(V)-isotherme of a Van der Waals gas exhibits at the critical temperature TK a saddlepoint (pK, Vk) when dp/dV = 0 and d2p/dV2 = 0.
![]() …
… ![]() …
… ![]()
The critical parameters of a real gas are used to define the reduced variables Tr, pr and Vr
![]() …
… ![]() …
… ![]()
which lead to the general Van der Waals equation independent of the type of gas
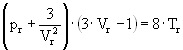
A detailed analysis of the experimental thermodynamic data for hydrogen by Hemmes et al has lead to propose an equation of state based on the modified Van der Waals equation [18] for 1 mol of hydrogen.
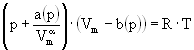
where b(p) is a pressure dependent excluded volume, a(p) a pressure dependent interaction term, a is approximately constant but not equal to two and Vm is the molar volume. The pressure dependencies are described by
![]() (p > 1 bar)
(p > 1 bar)
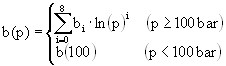
where p is measured in bar. For the weak temperature dependence of the power a a simple quadratic form was assumed.
![]() … for T £ 300 K
… for T £ 300 K
a(T) = a(300) …. for T ³ 300K
| a0 | 2.9315 | b0 | 20.285 |
| a1 | -1.531·10-3 | b1 | -7.44171 |
| a2 | 4.154·10-6 | b2 | 7.318565 |
| b3 | -3.463717 | ||
| b4 | 0.87372903 | ||
| a1 | 19.599 | b5 | -0.12385414 |
| a2 | -0.8946 | b6 | 9.8570583·10-3 |
| a3 | -18.608 | b7 | -4.1153723·10-4 |
| a4 | 2.6013 | b8 | 7.02499·10-6 |
Fig. Coefficients for the calculation of a(p), b(p) and a.
Fig. Reference isobar (p = 1 bar) for the temperature range 100K to 1000K.
From the EoS the changes in the thermodynamic quantities can be determined. In order to calculate absolute values we have to know the properties of hydrogen for some reference state e.g. the 1 bar reference isobar.
A large part of the experimental thermodynamic data on hydrogen is reproduced by the modified Van der Waals equation within 0.1% and practically all data within 0.5%.
The compressibility Z is often applied to correct for the non-ideal behaviour of real gases and is defined
![]()
![]()
With p(Vm) and Vm given by the EoS, the compressability can be calculated.
The Gibbs free energy G(p,T) is according to equation 6 for an ideal gas
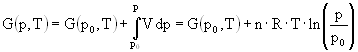
In order to correct for the non-ideal behaviour of the real gas the pressure is replaced by the fugacity f. The Gibbs free energy of a real gas is
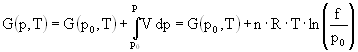
The fugacity coefficient f is defined as f = f/p and is independent of the standard pressure p0 (p0 = 1.013·105 Pa). The logarithm of the fugacity coefficient can be calculated [19] by means of the virial coefficients.
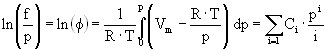
| T [K] | C1 | C2 | C3 | C4 | C5 |
| 60 | -3.54561·10-4 | 1.66337·10-7 | -2.99498·10-11 | 2.42574·10-15 | |
| 77 | -1.38130·10-4 | 4.67096·10-8 | 5.93690·10-12 | -3.24527·10-15 | 3.54211·10-19 |
| 93.15 | -3.86094·10-5 | 1.23153·10-8 | 9.00347·10-12 | -2.63262·10-15 | 2.40671·10-19 |
| 113.15 | 1.32755·10-5 | 1.01021·10-8 | 4.43987·10-13 | ||
| 133.15 | 3.59307·10-5 | 5.40741·10-9 | 4.34407·10-13 | ||
| 153.15 | 4.24489·10-5 | 5.03665·10-9 | 8.93238·10-14 | ||
| 173.15 | 4.29174·10-5 | 5.56911·10-9 | -2.11366·10-13 | ||
| 193.15 | 4.47329·10-5 | 3.91672·10-9 | -4.92797·10-14 | ||
| 213.15 | 4.34505·10-5 | 3.91417·10-9 | -1.50817·10-13 | ||
| 233.15 | 4.45773·10-5 | 2.18237·10-9 | 5.85180·10-14 | ||
| 253.15 | 4.48069·10-5 | 8.98684·10-10 | 2.03650·10-13 | ||
| 273.15 | 4.25722·10-5 | 9.50702·10-10 | 1.44169·10-13 | ||
| 293.15 | 3.69294·10-5 | 2.83279·10-9 | -1.93482·10-13 | ||
| 298.15 | 3.49641·10-5 | 3.60045·10-9 | -3.22724·10-13 | ||
| 313.15 | 4.16186·10-5 | -5.28484·10-10 | 2.73571·10-13 | ||
| 333.15 | 4.05294·10-5 | -7.21562·10-10 | 2.52962·10-13 |
Tab. Coefficients Ci as a function of temperature.
The relation between the compressibility and the fugacity is therefore
| p
[bar] |
Vm
[cm3·mol-1] |
H
[J·mol-1] |
G
[J·mol-1] |
S
[J·mol-1·K-1] |
| 1 | 24943.02 | 8506 | -30724 | 130.77 |
| 2 | 12485.87 | 8507 | -28994 | 125 |
| 5 | 5003.08 | 8510 | -26704 | 117.38 |
| 10 | 2508.87 | 8515 | -24968 | 111.61 |
| 20 | 1261.83 | 8526 | -23224 | 105.84 |
| 50 | 513.73 | 8560 | -20895 | 98.18 |
| 100 | 264.51 | 8620 | -19091 | 92.37 |
| 200 | 140.09 | 8747 | -17210 | 86.52 |
| 500 | 65.78 | 9176 | -14454 | 78.77 |
| 1000 | 40.98 | 9954 | -11924 | 72.93 |
| 2000 | 27.96 | 11529 | -8615 | 67.15 |
| 5000 | 18.75 | 15896 | -1962 | 59.53 |
| 10000 | 14.58 | 22319 | 6189 | 53.77 |
| 20000 | 11.56 | 33414 | 19013 | 48 |
| 50000 | 8.64 | 60517 | 48402 | 40.39 |
| 100000 | 6.84 | 94585 | 86094 | 28.31 |
| 200000 | 5.52 | 154070 | 146981 | 23.63 |
| 500000 | 4.1 | 293183 | 287378 | 19.35 |
| 1000000 | 3.23 | 472676 | 467424 | 17.51 |
Tab. The volume V, enthalpy H, Gibbs free energy G and entropy S of n-H2 at a temperature (T = 300 K) and pressures (p = 0.1 MPa – 100 GPa, i.e., 1·106 bar). The values are taken from Hemme et al. [20] The complete set of data for temperatures (T = 100 – 2000 K) can be found in Fukai [21] and Sugimoto [22]
Joule-Thomson effect, Inversion curve
The differential coefficient was first investigated by James Joule and William Thomson [23] in the 1850’s, before Thomson was elevated to the peerage, to became the first Baron Kelvin. So it is also referred to as the Joule-Kelvin coefficient.
![]()
It is a measure of the effect of the throttling process on a gas, when it is forced through a porous plug, or a small aperture or nozzle. The drop in pressure, at constant enthalpy H, has an effect on temperature. The enthalpy of hydrogen as a Van der Waals gas is given by the specific values (per mole) of the extensive variables H, and V, are written h and v.
![]()
where u is the inner energy, f is the degree of freedom (5 for H2) and v is the molar volume of the gas. The change of the enthalpy is given by the differential and is zero for an isenthalpic expansion
![]()
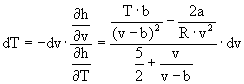
In a pressure-temperature plot, for any gas, the locus of points at which the drop in pressure, at constant enthalpy H, has no effect on the temperature is called the inversion curve for that gas. So the inversion curve has the simple form m = 0. These curves are plotted by first finding a family of isenthalpes (H = const.) on the T-p plane, then connecting their stationary points.) Except along the inversion curve, throttling either heats the gas (m < 0), or cools it (m > 0). Cooling of gases, in order to subsequently liquefy them, is usually accomplished by throttling in a region where it causes cooling.
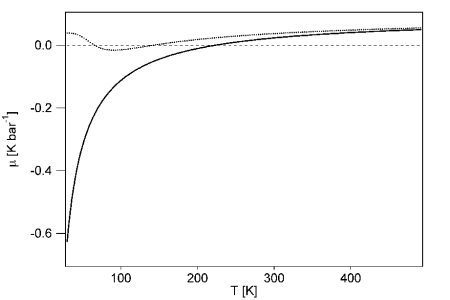
Fig. The Joule-Thomson coefficient for H2 in the Van der Waals approximation for a pressure of p = 0.1 MPa (solid line) and p = 10 MPa (dashed line).
The specific values (per mole) of the extensive variables H, S, and V, are written h, s, and v. Then the specific enthalpy [24] is
![]() and
and ![]()
Thus it follows that the Joule-Thomson coefficient is
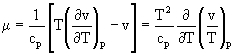
The first thing to notice about the Joule-Thomson coefficient is that it vanishes for an ideal gas. The inversion „curve“ is everywhere for an ideal gas! For real gases, the isenthalps have to be determined experimentally and the line connecting the stationary points is the inversion curve.
The simplest equation of state for a gas which predicts an inversion curve is the Van der Waals equation. It yields an inversion curve that is fairly close, but not exactly correct. The Van der Waals equation in reduced variables (Eq. 14) is used in the equation for the Joule-Thomson coefficient leads for m = 0 and substituting index r by i to
![]()
Substituting Vi with pi one finds
![]()
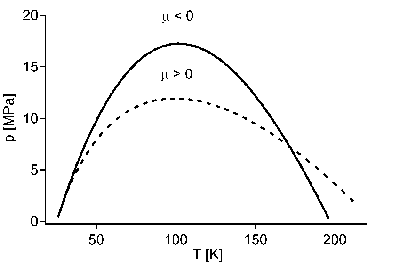
Fig. Inversion curve of n-hydrogen and calculated inversion curve using the critical pressure pk = 1.325 MPa and the critical temperature Tk = 33.19 K for hydrogen.
The two branches join at pi = 9, where Ti = 3 and Vi = 1. They connect this point with the Ti axis, wher pi vanishes, at the two points Ti = ¾ and Ti = 27/4. And of course, inside this curve is the region in which the Van der Waals equation predicts that throttling any gas will produce cooling.
Chemicals Properties and Diffusion
Hydrogen is the element with the highest diffusion capacity because of its small size and small mass. Some diffusion coefficients of hydrogen in gases and liquids are listed in the following table. In metals with a high hydrogen solubility usually also a high hydrogen diffusion rate is found. The diffusion coefficients [25] are in the same range as for hydrogen ions in water (10-4 cm2 s-1 at 25°C).
| Diffusion in | D [cm2 s-1] | T [°C] |
| N2 | 0.674 | 0 |
| O2 | 0.701 | 0 |
| H2 (selfdiffusion) | 1.285 | 0 |
| H2O, vapor | 0.759 | 0 |
| H2O, liquid | 4.8·10-5 | 25 |
| Iron, smelting | 5.64·10-3 | 1600 |
| Al, smelting | 1.28·10-5 | 960 |
| Palladium | 5.0·10-7 | 25 |
| Vanadium | 5.0·10-5 | 25 |
Tab. Diffusion coefficients of hydrogen in gases (p = 101.3 kPa) and liquids. [25]
Hydrogen has the electron configuration 1s1. The first electron shell can be filled with a maximum of two electrons. Therefore, the chemistry of hydrogen depends mainly on four processes:
(1) donate the valency electron to form the hydrogen ion, H*
(2 accept an electron to form the hydride ion H–
(3) share the electron with a partner atom to form a pair bond (covalent bond) H-H
(4) share the electron with an ensemble of atoms to form a metallic bond H0
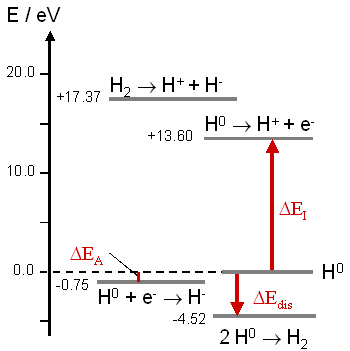
Fig. The different states of hydrogen and the corresponding transition energies.
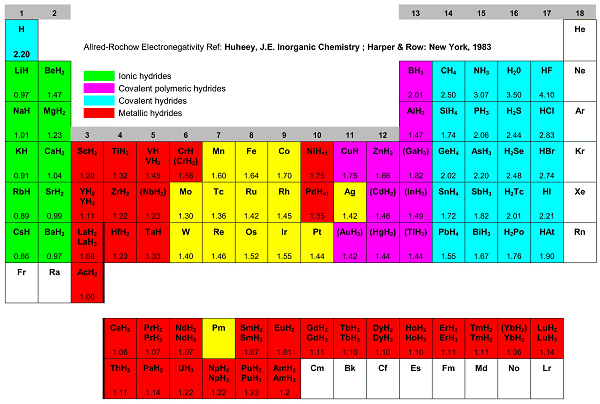
Fig. The different hydrides formed with the elements and their electronegativity (from left to right: ionic, metallic, polymeric covalent and covalent.
The degree of covalent to ionic character of the covalent bond depends on the electronegativity of the element to which hydrogen is attached. The electronegativity of hydrogen according to Pauli is 2.1. Except in the hydrogen molecule itself, where the bond is homopolar. all H -X bonds will possess some polar character. Hydrogen is not exceptionally reactive, although hydrogen atoms react with one another and with all other elements with the exception of the noble gases (only with helium short-lived instable forms such as HeH+ and HeH22+ are known). Hydrogen oxidizes less electronegative elements (e.g., alkali and alkaline earth metals), and reduces more electronegative ones (e.g., halogens, oxygen, nitrogen, carbon). The strength of the H-X bond in covalent hydrides depends on the electronegativity and size of the element X. The bond strength decreases in a group with increasing atomic number and generally increases across any period. The most stable covalent bonds are those formed between two hydrogen atoms (or isotopes), or with halogens, oxygen, carbon, and nitrogen.
| Bond | DH0298 [kJ·mol-1] | Bond | DH0298 [kJ·mol-1] |
| H-H | 282.4 | H-N | 314 |
| H-D | 440 | H-N= | 435.4 |
| D-D | 443.4 | H-O | 428.2 |
| T-T | 446 | H-OH | 498.1 |
| H-CH3 | 435.3 | H-S | 344.5 |
| H-C= | 452 | H-Cl | 431.6 |
| H-Cº | 536 | H-F | 568.9 |
Tab. Average bond dissociation energies of representative covalent hydrogen bonds at 298 K.
Halogens react with hydrogen to yield hydrogen halides, with increasing reactivity in the sequence iodine, bromine, chlorine, and fluorine. At –210°C liquid fluorine ignites immediately in hydrogen; solid fluorine explodes violently in the presence of liquid hydrogen; similarly, combined hydrogen reacts more or less violently with fluorine. Oxygen reacts with hydrogen according to
H2 + ½ O2 ® H2O …. DH0298 = -285 kJ·mol-1, S0 = 70 J·K-1·mol-1
Above 550°C the reaction occurs with flame propagation, explosion or detonation (oxyhydrogen reaction). The flame temperature is limited by the thermal dissociation of water vapor and attains a maximum of 2700°C.
At elevated temperatures in presence of suitable catalysts, hydrogen will react with nitrogen to form ammonia. Industrially this is one of the most important reactions.
3 H2 + N2 ® 2 NH3 …. DH0298 = -46 kJ·mol-1, S0 = 192 J·K-1·mol-1
Hydrogen reacts with carbon at high temperatures to yield methane. The equilibrium of the reaction is on the methane side at low temperatures, and on the hydrogen and carbon side at high temperatures.
2 H2 + C ® 2 CH4 …. DH0298 = -75 kJ·mol-1, S0 = 186 J·K-1·mol-1
The equilibrium constant, using graphite as a basis, is 2·105 bar at 150°C and 9.4·10-3 bar at 1000°C. Carbon monoxide and carbon dioxide can react with hydrogen in the presence of a catalyst. Depending on the reaction conditions, catalyst and CO:H2 ratio a variety of products can be formed. Unsaturated hydrocarbons are converted to saturated or partially saturated hydrocarbons by hydrogenation. In the petroleum industry hydrogenation and hydrocracking reactions are of importance as well as desulfurization and selective hydrogenation (dienes, monoolefins).
A great number of metals react with hydrogen to form hydrides. Depending on the nature of the hydrogen bond, hydrides are classified into four principal categories: covalent, ionic, complex and metallic.
The saline hydrides or ionic hydrides are formed when the strongly electropositive alkali metals and the alkaline earth metals (calcium, strontium, barium), all usually in the elemental form, react with hydrogen at high temperatures. Salt-like hydrides contain the hydride ion, H–; they are crystalline, have high heats of formation and high melting points. They are reactive, powerful reducing agents, all of them reacting with water to liberate hydrogen.
Covalent hydrides may be either solid, liquid or gaseous; typical are the hydrides of boron, aluminum, silicon. germanium and tin. Beryllium and magnesium hydride seem to represent a transition between ionic and covalent hydrides. The bond between hydrogen and the atom is of the nonpolar electron-sharing type. Molecular stability often is provided by means of three-centered two-electron bridge bonds (e.g., in diborane, B2H6, an electron-deficient type molecule), by hydride anion formation (BH4–, AlH4–), or formation of polymeric structures [polymeric (AlH3)x].
Metallic hydrides are formed by the transition metals. Transformation of a pure metal into a hydride occurs through continuous solution of hydrogen in the metal with subsequent abrupt phase transition at defined stoichiometric hydride phases (ZrH2, PdH. VH, VH2).
Substances containing hydrogen coupled to the most electronegativ elements exhibit properties that are best explained by assuming that the hydrogen atom of an H-X bond still has a small but significant affinity for other electronegative atoms although it remains strongly bonded to the original atom. This relatively weak secondary bond is called a hydrogen bond normally depicted by the notation X-H……Y. Hydrogen bonds result in molecular association. NH3, H2O, and HF have much higher boiling points and heats of vaporization than the corresponding homologues PH3, H2S.and HCl. Carboxylic acids such as acetic or benzoic acids are present as dimers with the configuration
The presence of hydrogen bonds also causes formation of crystalline hydrates such as NH3·H2O, SO2·H2O hydrocarbon hydrates (e.g., with natural gas components) as well as the zig-zag structure of the (HF)n polymer.
The existence of the hydrogen bond can be shown by infrared spectroscopy. When the hydrogen of the X-H group forms a hydrogen bond with the atom Y, the X-H stretching frequency is lowered and the absorption band characteristically broadened. In NMR spectroscopy a proton which participates in a hydrogen bond, produces a definite paramagnetic shift. The energies of hydrogen bonds are in the range of 4-40 kJ·mol-1, which is small as compared to 200-400 kJ·mol-1 for ordinary bonds. The average bond length is 200-300 pm (O-H…..O in ice 276 pm).
Atomic hydrogen is much more reactive than the molecular form. The dissociation reaction
H2 ® 2 H …. DH0298 = 432.2 kJ·mol-1
is highly endothermic. Atomic hydrogen can be produced thermally by supplying sufficient energy, e.g., in electric arcs with a high current density, electrical discharges at low pressures, irradiation with UV light as well as electron bombardment (10-20 eV). The hydrogen atom has a short half-life (ca. 0.3 s) and reacts even at room temperature with nonmetallic elements such as halogens, oxygen, sulfur. and phosphor to form the corresponding hydrogen compounds. At room temperature it reduces many oxides to the elements. The heat of recombination of hydrogen molecules from hydrogen atoms leads to very high temperatures (Langmuir flare, 4000 K). Atomic hydrogen can be absorbed in the metallic structure of some elements of the Group 8-10 (Fe, Co, Ni) of the periodic system. The suitability of many catalysts for reactions involving hydrogen is based on the dissociation and solubility of hydrogen in the atomic form. Hydrogen formed upon dissolution of metals in acids is very reactive at the moment of formation (nascent hydrogen), much more than normal hydrogen. This strong reduction capability is often explained by a short term formation of atomic hydrogen. Another explanation is the intermediate formation of a hydride-type compound which is very similar to Grignard compounds.
The ionization potential of the reaction
H(g) ® H+(g) + e– …. DH0298 = 1310 kJ·mol-1
which is even higher than the first ionization potential of the noble gas xenon. The hydrogen ion can be formed only in a medium which solvates the protons. The solvation process provides the energy required for bond rupture. the order of magnitude can be seen in the solvation reaction with water:
H+(g) + x H2O ® H+(aq) …. DH0298 = 1070 kJ·mol-1
In aqueous systems H3O+ is the form implied by the customary designation hydrogen ion. The structure of the H3O+ ion is that of a rather flat triangular pyramid with a H-O-H bond angle of ca. 110°, O-H bonds distances of 102 pm and a H-H distance of 172 pm. Normally, it is coordinated with four water molecules not all of which are equivalent, so that the aquated hydrogen ion is best represented as H9O4·H2O. The lifetime of an individual H3O+ ion is exceedingly short, l0-13 s, because the protons are rapidly exchanged among the water molecules.
In aqueous solutions the hydrogen ion activity is given in terms of the pH value, defined as –log(a(H+)), where a(H+) is the hydrogen ion activity. By definition, the potential of the redox system ½ H2(g) ® H+(aq) + e– is zero (E = 0.000 V) at all temperatures, when an inert metallic electrode is immersed in a solution of unit activity (i.e., pH = 0) in equilibrium with hydrogen gas at 100 kPa pressure. The electrode material is a small platinum foil or a wire, coated with finely dispersed platinum black and is placed partly in the solution and partly in the hydrogen atmosphere. This standard hydrogen electrode is the reference electrode of all other oxidation-reduction systems. The relation between the electrochemical potential E and the hydrogen partial pressure pH2 is
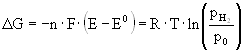
Ignition and detonation Performance
Hydrogen reacts, when the ignition energy (thermal activation energy) of » 0.02 mJ is provided, violently with oxidizing agents such as oxygen (air), fluorine or chlorine, and N2O. Combustion, deflagration or detonation may occur depending on the conditions. The ignition and detonation properties of hydrogen-air mixtures are particularly important from the safety aspect. The flammability limits (i.e., the minimum and the maximum concentration of hydrogen in air) are exceptionally wide for hydrogen.
| Hydrogen | Methane | Propane | Gasoline | |
| Density of gas at standard conditions [kg/m3(STP)] | 0.084 | 0.65 | 2.42 | 4.4a |
| Heat of vaporisation [kJ·kg-1] | 445.6 | 509.9 | 250-400 | |
| Lower heating value [kJ·kg-1] | 119.93·103 | 50.02·103 | 46.35·103 | 44.5·103 |
| Higher heating value[kJ·kg-1] | 141.8·103 | 55.3·103 | 50.41·103 | 48·103 |
| Thermal conductivity of gas at standard conditions [mW·cm-1 K-1] | 1.897 | 0.33 | 0.18 | 0.112 |
| Diffusion coefficient in air at standard conditions [cm2·s-1] | 0.61 | 0.16 | 0.12 | 0.05 |
| Flammability limits in air [vol%] | 4.0- 75 | 5.3-15 | 2.1-9.5 | 1-7.6 |
| Detonability limits in air [vol%] | 18.3-59 | 6.3-13.5 | 1.1-3.3 | |
| Limiting oxygen index [vol%] | 5 | 12.1 | 11.6b | |
| Stoichiometric composition in air [vol%] | 29.53 | 9.48 | 4.03 | 1.76 |
| Minimum energy for ignition in air [mJ] | 0.02 | 0.29 | 0.26 | 0.24 |
| Autoignition temperature [K] | 858 | 813 | 760 | 500-744 |
| Flame temperature in air [K] | 2318 | 2148 | 2385 | 2470 |
| Maximum burning velocity in air at standard conditions [m·s-1] | 3.46 | 0.45 | 0.47 | 1.76 |
| Detonation velocity in air at standard conditions [km·s-1] | 1.48-2.15 | 1.4-1.64 | 1.85 | 1.4-1.7c |
| Energyd of explosion, mass-related [gTNT/g] | 24 | 11 | 10 | 10 |
| Energyd of explosion, volume-related [gTNT·m3(STP)] | 2.02 | 7.03 | 20.5 | 44.2 |
Tab. Combustion and explosion properties of hydrogen, methane, propane and gasoline. a100 kPa and 15.5°C. bAverage value for a mixture of C1-C4 and higher hydrocarbons including benzene. cBased on the properties of n-pentane and benzene. d Theoretical explosive yields.
The above table shows a comparison of safety-relevant thermo-physical and combustion properties of hydrogen with those of methane, propane and gasoline [26]. The flammability limits are affected by the temperature, so that a preheated mixture has considerably wider limits for coherent flames [27]. An increase in pressures up to 10 kPa has only a small effect. Water vapor has a strongly inhibiting influence on the oxyhydrogen reaction.
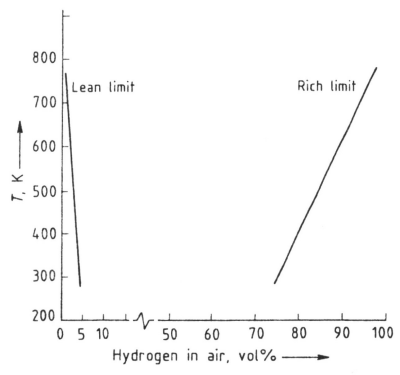
Fig. Effect of temperature on flammability limits of hydrogen in air (pressure 100 kPa)
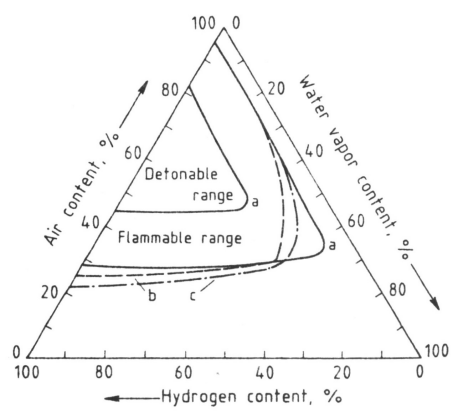
Fig. Flammability and detonability limits of the three component system hydrogen-air-water vapor [28] a42 °C, 100 kPa;b167°C, 100 kPa, c167°C, 800 kPa
The flammability limits of hydrogen in pure oxygen at room temperature are 4.65-93.9 vol% hydrogen, those of deuterium in pure oxygen 5.0-95 vol%. In general, the chemical properties of H, D, and T are essentially identical. Small differences can be found in processes where the atomic mass has a significant influence e.g. the thermal dissociation of a D-X bond requires a greater energy than for the comparable H-X bond.[29].
For comprehensive compilations of safety characteristics and hazards on handling hydrogen see ref.[30]. The envisaged large-scale introduction of hydrogen as an energy carrier requires a comparative evaluation of safety aspects with regard to fossil fuels. Volumetric leakage’s of hydrogen gas will be 1.3 -2.8 times as large as gaseous methane leakage and approximately four times that of air under the same conditions (rule: „airproof is not hydrogen-proof). Released hydrogen disperses rapidly by turbulent convection, drift and buoyancy, thus shortening the hazard duration. The prompt dispersion, however, favors the formation of gas mixtures within the wide flammability and detonability limits; the lower limit is the vital one in most applications and is comparable to that of other fuels. The minimum energy for ignition of hydrogen- air mixtures is extremely low. However, the ignition energy inherent in virtually every source is more than sufficient for ignition of any other fuel-air mixture as well. Ignition by catalytic action is also possible.
Fire Hazards. Hydrogen flames are nearly invisible in daylight. Hydrogen fires last only one fifth to one tenth of the time of hydrocarbon fires, and the fire damage is less severe because of several characteristics: 1) high burning rate resulting from rapid mixing and high propagation velocity, 2) high buoyant velocity, 3) high rate of vapor generation of liquid hydrogen. Although the maximum flame temperature is not much different from that of other fuels, the thermal energy radiated from the flame is only a part of that of a natural gas flame. Smoke inhalation, one of the major causes of injury and, therefore, a main parameter of fire damage, is considered less serious in the case of hydrogen because the sole combustion product is water vapor and some nitrogen oxides (depending on the temperature of the flame).
Explosive Hazards. High laminar burning velocity as well as the high laminar flame speed of hydrogen makes the transition to turbulent flame speeds exceeding 800 m·s-1 up to several km·s-1 easy. Hence, hydrogen is more sensitive to deflagration to detonation transition [31] (DDT) than hydrocarbons. Hydrogen has by far the widest limits of detonability; detonation of stoichiometric hydrogen-air mixtures in confined spaces will produce a static pressure rise of ca. 15:1. If a DDT process proceeds, i.e. unburned hydrogen-air mixtures are precompressed, a pressure rise ratio of 120:1 could result.
Explosions are rated in terms of the amount of energy released, commonly expressed as an equivalent quantity of Trinitrotoluene (TNT). The theoretical maximum values of explosive potential’s for fuels (TNT equivalents) are recorded in Table 2.1.7. Experimental data indicate, that real yield factors of l0% are considered reasonable. Note that hydrogen is most potent on a mass basis and least potent on a volumetric basis. It has also the least theoretical explosive potential, when equivalent energy storage is taken into account.
Preventive Measures.In safety concepts, distinctions are made between primary, secondary and tertiary measures. Primary safety precautions aim at the exclusion of causative risks such as leakage, formation of explosive mixtures by proper conceptual design (inertization, open-air installation, flame arrestors, etc.). Secondary measures consist mainly in the avoidance of ignition sources of any kind (electrostatically or mechanically generated sparks). Tertiary measures should minimise dangerous results in case fire or explosion occurs. This is achieved by installation of explosion- proof or explosion relief systems, hydrogen process shut-down systems and suitable fire extinguishing systems. Safety Regulations (mandatory) and standards (mandatory or nonmandatory) apply for the safe production, storage and handling of hydrogen. They are mostly concerned with transportation; other operations are covered by more general regulations.
Future Outlook. Considering the possible use of hydrogen in a future hydrogen energy carrier, no major safety problems are anticipated. Hydrogen has been handled successfully for decades in the process industries. Handling as a liquid is also routine. In comparison with other inflammable gases or liquids, the safety risk of hydrogen as a fuel is not significantly different.
Toxicology. Hydrogen does not show any physiological effect. It is nonpoisonous. Inhalation of the gas leads to sleepiness and a high-pitched voice. A danger of asphyxiation exists if the oxygen content sinks below 18 vol% because of hydrogen accumulation in the air. Direct skin contact with cold gaseous or liquid hydrogen leads to numbness and a whitish colouring of the skin and to frost bites. The risk is higher than, e.g., with liquid nitrogen because of the greater temperature differences and the higher thermal conductivity of hydrogen.
References
[1] Peter Häussinger, Reiner Lohmüller, Allan M. Watsin, “Ullmann’s Encyclopedia of Industrial Chemistry, Chap.: Hydrogen”, Fifth, Completely Revised Edition, Volume A13: High-Performance Fibers to Imidazole and Derivatives, VCH, pp. 297-442
[2] Handbook of Chemistry and Physics, Weast R. C., ed. 57th (1976), CRC Press
[3] Urey H C; Brickwedde F G; Murphy G M, “A Hydrogen Isotope of Mass 2 and its Concentration”, The Physical Review 40:1 (April 1 1932), p. 1-15
[4] M.L.E. Oliphant, P. Harteck and Lord Rutherford, Proc. Roy. Soc. London A 144 (1934), pp. 692
[5] A. Novick, “Half Life of Tritium”, Phys. Rev. 72, Letters to the Editor (1947), pp. 972
[6] I. F. Silvera, J. T. M. Walraven, Phys. Rev. Lett. 44 (1980), pp. 164
[7] I. F. Silvera, Rev. Mod. Phys. 52 (1980), pp. 393
[8] Massie, S. T. and Hunten, D. M. „Conversion of para and ortho Hydrogen in the Jovian Planets.“ Icarus 49 (1982), pp. 213-226
[9] N. S. Sullivan, D. Zhou and C. M. Edwards, Precise and efficient in situ ortho-para-hydrogen converter, Cryogenics 30 (1990), pp. 734
[10] S. Yucel, Theory of ortho-para conversion in hydrogen adsorbed on metal and paramagnetic surfaces at low temperatures, Phys. Rev. B 39 (1989), pp. 3104.
[11] V Diatschenko, C. W. Chu, D. H. Liebenberg, D. A. Young, M. Ross, R. L. Mills, “Melting curves of molecular hydrogen deuterium under high pressures between 20 and 373 K”, Physical Review B 32: 1 (JULY 1 1985), pp. 381-389
[12] W. B. Leung and N. H. March H. Motz, “Primitive Phase Diagramm for Hydrogen”, Physics Letters 56A, 6 (1976), pp. 425-426
[13] K. F. Mucker, D. White et al. Phys. Rev. Lett. 15 (1965), pp. 586
[14] I. F. Silvera, Rev. Mod. Phys. 52 (1980), pp. 393
[15] E. Wigner, H. B. Huntington, J. Chem. Phys. 3 (1935), pp. 764
[16] N. W. Asheroft, Phys. Rev. Lett. 21 (1968), pp. 1748
[17] H. Hemme, A. Driessen, R. Griessen, “Thermodynamic properties of hydrogen at pressures up to 1 Mbar and temperatures between 100 and 1000K”, J. Phys. C 19 (1986), pp. 3571-3585.
[18] H. Hemme, A. Driessen, R. Griessen, “Thermodynamic properties of hydrogen between 100 and 1000K at pressures up to 1 Mbar” Physica 139 & 140B (1986), pp. 116-118.
[19] Li Zhou and Yaping Zhou, “Determination of compressibility factor and fugacity coefficient of hydrogen in studies of adsorptive storage”, Int. J. Hydrogen Energy 26 (2001), pp. 597-601
[20] H. Hemme, A. Driessen, R. Griessen, “Thermodynamic properties of hydrogen at pressures up to 1 Mbar and temperatures between 100 and 1000K”, J. Phys. C 19 (1986), pp. 3571-3585.
[21] Yuh Fukai, “The Metal-Hydrogen System Basic Bulk Properties”, Springer Verlag Heidelberg, ISBN 3-540-55637-0.
[22] H. Sugimoto, Y. Fukai, Acta Metall. 40 (1992), pp. 2327.
[23] Joule, James P. and William Thomson. XV. „On the Thermal Effects of Fluids in Motion.-Part II.“ Philosophical Transactions 114 (1854): 321-364. Joule, James P. and William Thomson. XI. „On the Effects of Fluids in Motion.-No. II.“ Proceedings of the Royal Society 7 (1856): 127-130. Joule, James P. and William Thomson. XXV. „On the Thermal Effects of Fluids in Motion.- Part IV.“ Philosophical Transactions 152 (1862) 579-589.
[24] M.W. Zemansky, R.H. Dittman, „Heat and Thermodynamics“, 7th edition 1997, McGraw-Hill
[25] G. Holleck, J. Phys. Chem. 74 (1970), pp. 503
[26] J. Hord, Int. J. Hydrogen Energy 3 (1978), pp. 157
[27] I. L. Drell, F. E. Belles, “Survey of Hydrogen Combustion Properties”, NASA Report 1383, Washington D.C. 1952
[28] M. Fischer, H. Eichert, DFVLR-Nachr. 34 (1981), pp. 33
[29] K. B. Wiberg, Chem. Rev. 55 (1955), pp. 713
[30] NASA Lewis Research Center, “Hydrogen Safty Manual”, NASA Tech. Memo TM-X 52454 (1968); K. M. Kalyanam, D. R. Hay, “Safty Guide for Hydrogen”, National Research Counciel Hydrogen Safty Committee, Ottawa (1987); Frederick D. Gregory, “SAFETY STANDARD FOR HYDROGEN AND HYDROGEN SYSTEMS”, Guidelines for Hydrogen System Design, Materials Selection, Operations, Storage, and Transportation, Office of Safety and Mission Assurance, Washington, DC 20546, National Aeronautics and Space Administration NASA (1997).
[31] H. Eichert, M. Fischer, Int. J. Hydrogen Energy 11 (1986), pp. 117

